Une question revient souvent, que ce soit sur le groupe de discussion ou dans d’autres forums consacrés au modélisme naval. « Quel est le poids d’une maquette de bateau lorsqu’il est à une échelle 1/n » ou en d’autres termes : comment et de combien la mise à l’échelle d’un bateau va modifier les différents paramètres physiques qui le caractérisent.
Un peu d’analyse dimensionnelle
Quand on fait la maquette d’un bateau, il y a certains éléments qui ne subissent pas l’effet d’échelle :
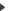 l’eau dans laquelle il évolue
l’eau dans laquelle il évolue
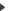 le temps (T)
le temps (T)
Et d’autres qui le subissent :
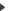 Les dimensions du navire (L)
Les dimensions du navire (L)
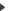 Sa masse (M)
Sa masse (M)
Le volume du navire est en L au cube (L3). le volume d’eau déplacé pour que le navire soit « dans ses lignes » aussi. Donc, quand on met à l’échelle E, le volume d’eau déplacé va être divisé par E3. La masse volumique de l’eau étant constante (pour une salinité donnée), la masse doit aussi être divisée par E3.
Il ne s’agit pas d’une approximation, c’est un calcul exact.
Exemple : un bateau de 10000 tonnes (10000000 kg) réalisé au 1/50e aura une masse, à l’échelle, égale à 10000000 /(50×50×50) = 80 kg.
Pour un bateau de 18 tonnes réalisé au 1/15, on aura : 18 tonnes /15x15x15 (donc 18000 divisé par 3375) = 5,3 kgs
On en vient à l’analyse dimensionnelle : toute grandeur physique a une dimension exprimée en fonction des dimension des grandeurs de base :
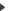 L : longueur
L : longueur
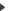 M : masse
M : masse
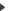 T : temps
T : temps
Il y en a 4 autres mais elles ne concernent pas la mécanique (au sens physique du terme). On a donc :
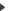 Une surface : L2
Une surface : L2
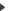 Un volume : L3
Un volume : L3
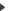 Une vitesse : L/T
Une vitesse : L/T
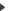 Une force : M×L/T2
Une force : M×L/T2
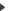 Une énergie : M×L2/T2
Une énergie : M×L2/T2
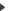 Une puissance : M×L2/T3
Une puissance : M×L2/T3
Finalement, à quelle vitesse doit aller une maquette ?
Si on calcule strictement la vitesse d’un modèle selon la dimension de la vitesse, on en conclut que celle-ci doit être divisée (par rapport au bateau réel) par l’échelle. Donc, la maquette au 1/15e d’un chalutier qui marche a 10 noeuds devrait filer 10/15 = 0,66 noeuds. La maquette au 1/100e d’un destroyer qui marche à 35 noeuds devrait filer 0,35 noeuds (50 cm/s). Si on procède de cette manière, on constatera que la maquette n’a pas l’allure escomptée sur l’eau. En effet, l’impression de vitesse vient essentiellement de la forme de la vague d’étrave, c’est à dire de l’allure de l’écoulement de l’eau autour de la coque et l’eau ne subit pas l’effet d’échelle. Pour avoir une vitesse réaliste, il faut donc que les écoulements soient similaires.
Une coque qui se déplace sur l’eau va rencontrer deux types de résistance :
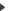 l’eau frotte sur la coque
l’eau frotte sur la coque
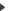 la coque « déplace » de l’eau
la coque « déplace » de l’eau
On va donc avoir deux forces qui vont s’opposer au déplacement de la coque : une force de friction et une force de résistance à la vague. Dans le second cas, on voit que le bateau « pousse de l’eau » ce qui a pour effet de générer une vague d’étrave.
C’est cette dernière force qui nous intéresse. La similitude entre l’écoulement sur le vrai bateau et sur la maquette est mesurée par le Nombre de Froude :
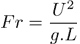
ou U est la vitesse, g l’accélération de la pesanteur et L la longueur immergée (flottaison).
Le but est de garder Fr constant et de calculer la vitesse du modèle. Le lecteur intéressé par le développement consultera l’encadré ci-contre. En résumé, La vitesse du modèle est celle de l’original divisée par la racine carrée de l’échelle (CQFD).
Reprenons notre bateau de 18 tonnes au 1/15eme qui dans la réalité a une vitesse de pointe de 25 noeuds et une vitesse de croisière de 20 noeuds cela donne 25 noeuds divisé par la racine carrée de 15 donc 46,3 kmh divisés par 3,9 = 11 kmh de vitesse maxi, et 37 divisé par 3,9= 9,5 kmh de vitesse de croisière
Bon calculs !
